| S.No | Question | Option A | Option B | Option C | Option D | Answer | Solution | Comments | Status | Action |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | According to Stefan Boltzman law the relation between the total emission from a black body per unit area and per unit time (Eb) and the absolute temperature (T) is given as | \(E_{b}âˆT^{4}\) | \(E_{b}âˆT^{3}\) | \(E_{b}âˆT^{2}\) | \(E_{b}âˆT\) | a | \( E_{b}âˆT^{4}\) \(=E_{b}=σT^{4}\) \(σ=Stephan boltzman constant \) |
Comments | Active | |
| 2 | The opaque body is that which | Absorbs all radiations | Reflects all radiations | Transmits all radiations | Partly reflects and partly absorbs the radiation | b | For opaque body, Reflectivity = 1, Absorptivity = transmissivity = 0, i.e. all the radiation from opaque surface will be reflected. | Comments | Active | |
| 3 | According to Newton’s law of cooling, the rate of heat transfer from a solid surface of area A, at a temperature , to a fluid at temperature is given by \(t_{1}\) \(t_{2}\) | Q = hA (t1+t2) | Q = hA (t1-t2) | Q = h / A (t1-t2) | Q = A / h (t1+t2) | b | We can use Newton’s law of cooling in convection and mathematically it is given by \(Q=hA∆T\) \(Q=rate of conductive heat transfer\) h = Coefficient of convective heat transfer A = Area exposed to heat transfer power is always unity. \(∆T=T_{S}-T_{F}\) \(T_{S}=Surface temperature \) \(T_{F}=Fluid temperature\) So, the temperature gradient has always unity power. |
Comments | Active | |
| 4 | According to Fourier’s law, the quantity of heat flow through a surface area ‘A’ and thickness ‘x’ is given by the relation | Q = - KA (dt/dx) | Q = - A/k (dt/dx) | Q = - A (dx/dt) | Q = - KA (dx/dt) | a | It says that the rate of transfer of heat across a substance is directly proportional to the negative gradient in temperature and area. \(Q=-KA\frac{dT}{dx}\) |
Comments | Active | |
| 5 | In which case the medium is not required for the transfer of heat energy | Conduction | Convection | Radiation | None of the above | c | Radiation: ​It transfers heat in the form of electromagnetic waves. It can heat any form of material. No need for a medium. | Comments | Active | |
| 6 | Heat conduction in gases is due to | The elastic impacts of molecules | The motion of electrons | The mixing motion of different parts of a fluid | The electromagnetic waves | a | In gases, heat transfer occurs through collisions of gas molecules with one another. The thermal conductivity of the liquids is more than the gasses and the metals have the highest. In the gaseous state, the molecules of a substance are spaced relatively far away, and their motion is random. This means that energy transfer by molecular impact is much slower than in the case of a liquid, in which the motion is still random but in liquids, the molecules are more closely packed. |
Comments | Active | |
| 7 | The process in which heat energy is transmitted by means of electromagnetic waves is known as | Heat conduction | Heat convection | Heat radiation | None of the above | c | Thermal radiation is the electromagnetic radiation emitted by a body with a temperature above absolute zero. The amount of energy emitted depends on the temperature of the surface and its ability to emit energy. | Comments | Active | |
| 8 | Beyond the stall point, the drag coefficient | Decreases rapidly | Increases rapidly | Remains same | None of the above | a | In fluid dynamics a stall is a reduction in the lift coefficient generated by a foil as angle of attack increases. This occurs when the critical angle of attack to the foil is exceeded. The critical angle of attack is typically about 15°, but it may vary significantly depending on the fluid, foil and Reynolds number. | Comments | Active | |
| 9 | The aspect ratio of a wing is expressed as | I/A | \(I/A^{2}\) | /A \(I^{2}\) | \(I^{2}/A^{2}\) | c | The wing area is a projected area and is almost half of the total surface area. Aspect ratio is a measure of now long and slender a wing is from tip to tip. The aspect ratio of a wing is defined to be the square of the span divided by the wing area and is given the symbol AR.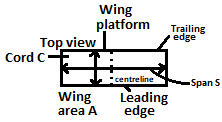    Aspect ratio = AR \(AR=\frac{S^{2}}{A}\) \(AR=\frac{S}{C} for rectangle\) |
Comments | Active | |
| 10 | The coefficient of drag and lift are functions of | Froude’s number | Reynold’s number | Weber’s number | Euler’s number | b | This lift coefficient is a dimensionless coefficient that relates the lift generated by a lifting body to the fluid density around the body, the fluid velocity and an associated reference are(a) The drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. Both of these coefficient depend on velocity characteristic length and density so these became a function of Reynolds number. |
Comments | Active | |
| 11 | The total drag on a plate held normal to the flow is equal to | Pressure drag | Viscous drag Viscous drag | Pressure drag x viscous drag | Pressure drag | a | Drag is defined as forceful pull experienced by the flat plate while the fluid flows over it. Pressure drag comes from the eddying motions that are set up in the fluid by the passage of the body. This drag is associated with the formation of a wake in the flow frictional drag comes from friction between the fluid and the surfaces over which it is flowing. For the plate held normal to flow. Fluid flows across and there’s huge wake formation occurring behind the plate. As the fluid is not flowing anywhere tangentially to the plate, there is negligible or no viscous drag experience(d) So, the total drag on a plate held normal to the flow is equal to pressure drag only. Figure A Plate held parallel to the flow – only viscous drag takes place.  Plate held normal to the flow only pressure drag takes place. |
Comments | Active | |
| 12 | The flow within the boundary layer is | Only turbulent | Only laminar | Either (a) or (b) | None of the above | c | A very thin layer of fluid in the immediate neighborhood of the solid boundary, where the variation of velocity from zero at the solid boundary to the free stream velocity in the direction normal to the boundary takes place is known as the boundary layer. In this layer, the flow is viscous and rotational.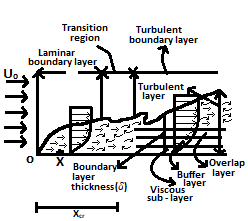 The flow within the boundary layer is either laminar or turbulent. |
Comments | Active | |
| 13 | The thickness of boundary layer is proportional to | Its distance from the leading edge | Square of its distance from the leading edge | Four times its distance from the leading edge | Square root of its distance from the leading edge | d | The boundary layer is the layer of fluid near a solid boundary where viscous effects become significant. It's characterized by a lower velocity than the outer layer, as well as turbulence and friction. Boundary layers may be laminar or turbulent, with transition occurring somewhere along the surface. The thickness of the boundary layer is the distance from the wall to the point where the velocity is 99 percent of the free stream. The growth of the boundary layer thickness in fluids is an essential concept. The boundary layer thickness grows as the square root of the distance from the leading edge. This is known as the boundary layer growth rule and is expressed as δ ∠x1/2. The boundary layer thickness grows in proportion with the square root of the distance from the leading edge, | Comments | Active | |
| 14 | The similarity of shape between the model and prototype is known as | Dynamic similarity | Kinematic similarity | Geometric similarity | None of the above | c | Shape will be same but size will be different. This similarity is known as geometrical similarity. | Comments | Active | |
| 15 | In a laminar flow, the velocity at any point is | Constant in magnitude but varying in direction | Constant in magnitude as well as in direction | Constant in direction but varying in magnitude | Variable in magnitude as well as in direction | a | Laminar flow is characterized by smooth flow of the fluid in layers that do not mix. Flow is proportional to pressure difference and inversely proportional to resistance. The flow of a viscous fluid in which particles of the fluid move in parallel layers, each of which has a constant velocity but is in motion relative to its neighboring layers. | Comments | Active | |
| 16 | The head loss due to turbulent flow as compared to laminar flow is | More | Less | Equal | Unpredictable | a | In case of laminar flow, the loss of pressure head was found to be proportional to the velocity but in turbulent flow. Reynolds observed that loss of head is approximately proportional to the square of velocity. | Comments | Active | |
| 17 | The velocity at which the flow changes from laminar to turbulent for a given fluid at a given temperature is known as | Maximum velocity | Minimum velocity | Average velocity | Critical velocity | d | Critical velocity occur when Reynold’s number is 2300. But in practice we take critical value of Re as 2000. | Comments | Active | |
| 18 | The frictional resistance in case of turbulent flow is independent of | Pressure of flow | Density of fluid | Temperature of fluid | Area of surface in contact | a | Frictional resistance in a flow increases if the contact of the fluid increases with the boundary surface, for turbulent flow, turbulent shear stress at the contact surface is directly proportional to the density of the fluid. Frictional pressure drop (Darcy – Weishbach Eq) \(h_{f}=fLv^{2}/2gD, f=0.\frac{0791}{Re^{\frac{1}{4}}}\) Therefore, frictional resistance for turbulent flow is directly proportional to the density of the fluid. Increase in the temperature decreases the viscosity of the fluid and hence decrease in frictional resistance. The pressure at a section in a fluid does not effects frictional resistance for a turbulent flow. |
Comments | Active | |
| 19 | An engine working on stirling cycle between the same temperature limits as that of Carnot cycle, has air standard efficiency | More than Carnot cycle | Equal to Carnot cycle | Less than Carnot cycle | Depends upon other factor also | b | The carnot cycle is a theoretical rather than a practical cycle, has the maximum possible efficiency of any cycle. There is a theoretical stirling cycle that is also reversible, which means that it would have the same efficiency as the carnot cycle, However, neither cycle can be realized in the real world, so a real stirling cycle will have a lower efficiency than the theoretical carnot cycle. | Comments | Active | |
| 20 | Constant volume cycle is also known as | Otto cycle | Joule cycle | Rankin cycle | Atkinson cycle | a | The air standard otto cycle is the idealized cycle for the spark ignition internal combustion engines. Otto cycle is the one which has two constant volume heat transfer processes and two adiabatic work transfer processes. | Comments | Active | |
| 21 | The velocity components in a two dimensional flow field for an incompressible fluid are expressed as u = + 2x – x2y= xy2 - 2y - \(ʋ \) These functions represent |
Rotational flow | Irrotational flow | Either rotational or irrotational flow | neither rotational nor irrotational flow | * | insufficient data To solve this if \(ω_{z}=\frac{1}{2}(\frac{∂v}{∂x}-\frac{∂u}{∂y})=0\) (Rotational component along z – axis) Flow will irrotational |
Comments | Active | |
| 22 | For an incompressible flow, which of the following is correct? | + = 0 \(\frac{∂u}{∂x} \) \(\frac{∂v}{∂y}\) | + > 0 \( \frac{∂u}{∂x} \) \(\frac{∂v}{∂y} \) | + < 0 \(\frac{∂u}{∂x} \) \(\frac{∂v}{∂y} \) | + = 1 \(\frac{∂u}{∂x}\) \(\frac{∂v}{∂y} \) | a | Continuity eqn for 2D flow, \(\frac{∂u}{∂x}+\frac{∂v}{∂y}=0\) | Comments | Active | |
| 23 | In case of multi-stage vapour compression system, flash intercooling is beneficial in case of those refrigerants only for which | Latent heat of vapourization is more | Latent heat of vapourization is less | Thermal conductivity is high | Thermal conductivity is low | a | 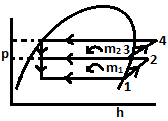 For high latent heat refrigerant, during flash cooling mass evaporated will be very less and isentropic process 1 – 2, 3 – 4 becomes flat hence power requirement decreases. Eg: NH3 |
Comments | Active | |
| 24 | Which of the following expression correctly defines the relationship between internal pressure intensity (p) and the radius of spherical droplet (r)? | p \(âˆ\frac{1}{r}\) | \( pâˆr\) | p \( âˆ\frac{1}{r^{2}}\) | p r2 \( âˆ\) | a | When a liquid and gas or two immiscible liquids are in contact, an unbalanced force is developed at the interface stretched over the entire fluid mass. The intensity of molecular attraction per unit length along any line in the surface is called as surface tension. For example in a spherical liquid droplet of radius (r), the pressure difference between the inside and outside surface of the droplet is given by so we can say that \((∆P)\) \(∆P=\frac{2σ}{r},\) \(pâˆ\frac{1}{r}.\) | Comments | Active | |
| 25 | What will be the depth of a point below water surface in sea, where pressure intensity is 1.006 MN/m2? (Specific gravity of sea water = 1.025) |
10 m | 100 m | 1000 m | 1 m | b | According to hydrostatic law \(P=Ïgh\) \(h=\frac{P}{Ïg}\) \(h=\frac{1.006×10^{6}}{1000×10}=100 m\) |
Comments | Active | |
| 26 | Actual expansion process in a throttling device is | Reversible adiabatic expansion | Isenthalpic expansion | Fanno - line expansion | Isothermal expansion | b | Throttling process is process in which a high pressure fluid is converted to low pressure fluid at constant pressure using a throttle valve. In throttling process, work done is zero & enthalpy is constant. It is an irreversible process. Joule’s Thomson coefficient \((μ)=\frac{dT}{dP} at constant H.\) |
Comments | Active | |
| 27 | Normal boiling point of different refrigerants are given below. Which pairs are correct? (1) NH3– 40.8°C (2) R-12– 29.8°C (3) R-22– 33.3°C (4) R-134a– 26.2°C |
(1) and (2) are correct | (3) and (4) are correct | (2) and (4) are correct | (1) and (4) are correct | c | Ammonia/Boiling point -33.34℃ Dichlorodifluouro methane/BP, R – 12 - 29.8℃ Chlorodiflouromethane/(B)P, R – 22 - 40.8℃ Tetrafluoroethane/(B)P. R – 134a – 26.2℃ |
Comments | Active | |
| 28 | Effective temperature in respect of air conditioning is the temperature of | Unsaturated air | Saturated air | Dry air | Either (b) or (c) above | d | Temperature of saturated or dry air is counted in (A)(C) | Comments | Active | |
| 29 | In winter air conditioning, the inside design conditions are given by the following | 25°C DBT, 50% RH | 25°C DBT, 60% RH | 21°C DBT, 50% RH | 21°C DBT, 60% RH | d | In winter comfort conditions \(21℃ DBT, 60% RH\) In summer comfort conditions \(=25℃ DBT, 50% RH\) |
Comments | Active | |
| 30 | Triple point and critical point pressure of carbon dioxide are | 4.58mm Hg and 221.2 bar respectively | 5.18 bar and 221.2 bar respectively | 1 bar and 50 bar respectively | 5.18 bar and 73.8 bar respectively | d | Comments | Active | ||
| 31 | Dittus – Boelter equation for heating of a fluid in a tube is given as follows | Nu=0.023 Re0.8 Pr0.4 | Nu=0.023 Re0.8 Pr0.3 | Nu=C Ren (where C is a constant and n is a real number) | Nu=C loge Ren | a | For fully developed (Hydrodynamically and thermally) turbulent flow in a smooth. Circular tube, the local. Nusselt number may be obtained from the well known dittus – boelter eqn. This dittus Boelter equation is easy to solve but is less accurate when there is a large temperature difference across the fluid and is less accurate for rough tubes. (many commercial applications), since it is tailored to smooth tubes. The Dittus Boelter co – relation may be used for small to moderate temperature differences, Twall – Tavg with all properties evaluated at an averaged temperature Tavg. Co – relation – dittus Boelter \(Nu_{DH}=0.023 REDh0.8 Pr^{0.4}\) Where Dh is the hydraulic diameter [m] Re is the Reynolds number [-] Pr is the Prandtl number [-] Nu is the Nusselt number [-] Validity \(0.6≤Pr ≤160\) \(Re_{Dh}>10000\) \(\frac{L}{D}>10\) |
Comments | Active | |
| 32 | For a double pipe, counter flow heat exchanger with C = 1 (C = Cmin / Cmax) the effectiveness is equal to | \(\frac{NTU}{NTU-1}\) | \( \frac{1+1}{NTU}\) | \(\frac{NTU}{NTU+1}\) | \( \frac{NTU+1}{NTU-1}\) | c | For a double pipe, counter flow heat exchanger with C = 1 (C = Cmin / Cmax) the effectiveness is equal to \(\frac{NTU}{NTU+1}\) |
Comments | Active | |
| 33 | Three radiation shields are placed between two infinite parallel plates. The emissivities of plates and shields are same. As compared to heat transfer without shields, the heat transfer with shield will become | \(\frac{1}{3}\) | \(\frac{1}{9}\) | \(\frac{1}{4}\) | None of the above | c | Just remember this formula for n – shielding plates. Net heat transfer with shields Qnet with shield = \(1/(n+1)×Q_{net} without shield\) \(=1/(3H)×Q_{net}without shield\) \(=\frac{1}{4}×Q_{net} without shield\) |
Comments | Active | |
| 34 | Radiations are incident from a small area to a disc of diameter D kept at a distance R. \(dA_{1}\) \(A_{2}\) The shape factor \(F_{dA_{1}-A_{2}}\) |
\(\frac{D^{2}}{R^{2 }+ D^{2}}\) | \(\frac{D^{2}}{4R^{2}+3D^{2}}\) | \(\frac{D^{2}}{4R^{2}+D^{2}}\) | \(\frac{D^{2}}{R^{2 }+4 D^{2}}\) | c | 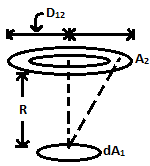 \(=R^{2}+(\frac{D}{2})^{2}\) \(=4R^{2}+D^{2}\) \(*F_{12}=\frac{A_{2}}{A_{1}} F^{21}\) (2 is so small F22=1) \(F_{12}=\frac{(D/2)^2 }{R^{2}+(D/2)^2 }\) \(F_{12}=\frac{D^{2}}{4R^{2}+D^{2}}\) |
Comments | Active | |
| 35 | For mixed (free and forced) convection in horizontal tubes of diameter d and length L, Graetz number (Gz) is defined as | Re. Pr. \(\frac{d}{L}\) | Gr. Re. . \(\frac{d}{L}\) | Gr. Pr. Re. \(\frac{d}{L}\) | Gr. Pr. \(\frac{d}{L}\) | a | In fluid dynamics, the Graetz number (Gz) is a dimensionless number that characterizes laminar flow in a conduit. The number is defined as. \(Gz=(\frac{D_{H}}{L})Re.Pr.\) is the diameter in round tubes or hydraulic diameter in arbitrary cross – section ducts L is the length. \(D_{H}\) Re is the Reynolds number Pr is the Prandtl number This number is useful in determining the thermally developing flow entrance length in ducts. A graetz number of approximately 1000 or less is the point at which the flow is would be considered thermally fully developed. When used in connection with mass transfer the prandtl number is replace by the schemidt number, Sc, which expresses the ratio of the momentum diffusivity to the mass – diffusivity. Gz = Re.Sc. \((D_{H}/L)\) |
Comments | Active | |
| 36 | The significance of Reynold analogy is that it | Tells whether flow is laminar or turbulent | Relates heat transfer to momentum transfer | Relates heat transfer and mass transfer | Relates heat transfer and frictional loss | b | It relates heat transfer and momentum transfer. \(\frac{Nu_{x}}{Re_{x}Pr_{x}}.Pr^{2/3}=\frac{C_{f}_{x}}{2}\) \([Local dimensionless numbers\)] |
Comments | Active | |
| 37 | Prandtl number is connecting link between | Velocity field and temperature field | Gravity field and temperature field | Gravity field and velocity field | None of the above | a | \( P_{r}=\frac{Momentum diffusivity}{Thermal diffusivity}\) Momentum means velocity field and thermal means temperature field. |
Comments | Active | |
| 38 | Air at 300 °C and 7 bar is expanded isentropically until the velocity is 300 m/s. Calculate the static temperature of the air at high velocity condition if CP of air is 1.00 kJ/kg-°C | 255 °C | 295 °C | 300 °C | None of the above | c | Stagnation temp \(t_{2}=t_{1}-\frac{C22}{2000.C_{P}}\) \(=300-\frac{(300)^{2}}{2000×1}\) \(=300-45=255℃\) |
Comments | Active | |
| 39 | General conduction equation in its simple form, (where T is temperature), is called \(∇^{2}T=0 \) | Poisson’s equation | Fourier’s equation | Laplace equation | Kirchoff’s equation | c | Laplace eqn Discussed earlier |
Comments | Active | |
| 40 | In transient heat conduction, lumped capacity analysis is applicable with good accuracy when Biot number (Bi) | is equal to 1 | is less than 0.1 | is greater than 0.1 | is less than 1 | c | Comments | Active | ||
| 41 | Consider a cylinder of radius R with uniformly distributed heat source of heat generation rate and constant thermal conductivity K. Assume temperature as a function of radius (r) only. The boundary conditions are; T = Tw at r = R and heat generated equals heat lost at surface. The temperature distribution in the cylinder is given by |
T = Tw + ( 1- \(\frac{q}{2k}\) \(\frac{r^{2}}{R^{2}})\) | T = Tw + ( 1- \(\frac{q}{4k}\) \(\frac{r^{2}}{R^{2}})\) | T = Tw + (R2- r2 \(\frac{q}{2k}\) \()\) | T = Tw + (R2- r2 \(\frac{q}{4k}\) \()\) | b | Just remember it. Don’t go for derivation. | Comments | Active | |
| 42 | With the increase in the length of fin, fin efficiency | Decreases | Increases | Remains unaffected | First increases and then decreases | a | The fin efficiency defined as the ratio of the heat transfer to the fin to the heat transfer to an ideal fin. It can be increased by increasing thermal conductivity K, or increasing fin width B, or by decreasing convective heat transfer coefficient ‘n’ or decreasing length of fin ‘L’. | Comments | Active | |
| 43 | Euler number is given as the ratio of | Inertia force / Gravity force | Pressure force / inertia force | Inertia force / Surface tension | Gravity force / Inertia force | * | \( Eu=\frac{Inertia force}{Pressure force}\) Euler number is a dimensionless value for analyzing fluid flow dynamics problems where the pressure difference between two points is important. The Euler number can be interpreted as a measure of the ratio of the inertia force to the pressure forces. |
Comments | Active | |
| 44 | Impingement of a jet on a flat plate may be expressed by | ψ = xy | ψ = x2 – y2 | = x3 + y3 \(ψ \) | ψ = x / y | a | Stream function for fluid jet \(Ψ=xy\) (Remember direct) |
Comments | Active | |
| 45 | Flow over an elliptical body may be idealized by superimposing a free stream and | A source | A doublet | A source and sink | A free vortex | c | 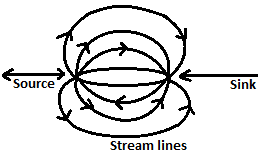 |
Comments | Active | |
| 46 | A normal shock can occur only when | Flow changes from supersonic to subsonic | Flow changes from sonic to subsonic | Flow changes from subsonic to sonic | The flow is Trans-sonic | a | A normal shock occurs as front of a supersonic object if the flow is turned by a large amount and the shock cannot remain attached to the body. The detached shock occurs for both wedges and cones. A normal shock is also present in most supersonic inlets, “Normal shocks†are a fundamental type of shock wave. The waves, which are perpendicular to the flow, are called normal shock. Normal shocks only happen when the flow is supersonic At those speeds, no obstacle is identified before the speed of sound which makes the molecule return after sensing the obstacle. | Comments | Active | |
| 47 | The critical angle of attack of an aerofoil is that where | The lift becomes zero | The drag becomes zero | The drag begins to rise | The lift begins to drop | d | The critical angle of attack is the angle of attack which produces the maximum lift coefficient. Below the critical angle of attack, as the angle of attack decreases, the left coefficient decreases. Conversely above the critical angle of attacks, as the angle of attack increases, the air begins to flow less smoothly over the upper surface of the airfoil and begins to separate from the upper surface. The angle of attacks of an airfoil at which the flow of air about the airfoil at which the flow of air about the airfoil changes abruptly so that lift is sharply reduced and drag is sharply increased.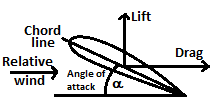 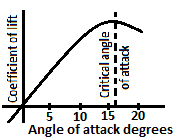 Also known as stalling angle of attack. The lift produced by an airfoil is the net force produced perpendicular to the relative wind. The drag incurred by an airfoil is the net force produced parallel to the relative win(d) The angle of attack is the angle between the chord line and the relative win(d) The critical or stalling angle of attack is typically around 15° - 20° for many airfoils. |
Comments | Active | |
| 48 | In case of flow over a flat plate, the Reynold number at which flow becomes turbulent is | 2300 | 3.2x105 | 7.5x105 | 2000 | c | Comments | Active | ||
| 49 | Flow separation is caused by | Reduction of pressure in the direction of flow | Reduction of the boundary layer thickness | Presence of adverse pressure gradient | Presence of favourable pressure gradient | c | An adverse pressure gradient \((\frac{∂P}{∂x}>0)\) When the pressure goes increasing in the direction of flow, the pressure force acts against the direction of flow thus retarding the flow. This has an effect of retarding the flow in the boundary layer and hence thickenings the boundary layer more rapidly. This and the boundary shear bring the fluid in the boundary layer to rest and causes back flow. Due to this the boundary layer no more sticks to the boundary but is shifted away from the boundary. This phenomenon is called “Boundary layer separationâ€. |
Comments | Active | |
| 50 | The flow in the capillary tube is laminar because | The capillary tube is made of glass | The surface tension and capillarity promotes laminarisation | Only inviscid liquid can flow through capillary tube | The diameter of capillary tube is very small | d | Since diameter is very small of capillary tube so distance between boundaries of tube is very small. Near boundary viscous flow will be laminar here. | Comments | Active | |
| 51 | A small air bubble of diameter 1.0 mm rises with a steady velocity of 1.5 cm/s through an oil of specific gravity 0.9. The viscosity of oil will be | 3.24x10-3 N-s/m2 | 32.4x10-3 N-s/m2 | 32.4x10-6 N-s/m2 | None of the above | b | Terminal velocity \(ν=\frac{2r^{2}Ïg}{9η}\) \(η=viscosity\) \(1.5×10^{-2}=\frac{2×(0.5×10^{-3})^{2}×9000×9.81}{9×η}\) \(η=32.4×10^{-3} N-S/m^{2}\) |
Comments | Active | |
| 52 | A 20 cm diameter pipe of 30 km length transports oil at 0.01 m3/s. The power required to maintain flow will be [µ = 0.1N - s/m 3 , density = 900kg/m 3 ] | 76.32 kW | 7.632 kW | 763.2 W | 0.7632 kW | b | \( Power P=\frac{128 μQ^{2}L}{πD^{4}}\) \(=\frac{128×0.1×0.01^{2}×30×10^{3}}{π(20×10^{-2})^{2}}\) \(=7632 W\) \(=7.632 kW\) |
Comments | Active | |
| 53 | Third law of thermodynamics is | An extension of second law | An extension of first law | An independent law of nature | An extension of zeroth law | a | Entropy is introduced by 2nd law of thermodynamics. The third law of thermodynamic states that the entropy of a system approaches a constant value as the temperature approaches absolute zero. An example that states the third law of thermodynamics is vapours of water are the gaseous forms of water at high temperature. | Comments | Active | |
| 54 | Which cycle consists of three processes? | Ericsson cycle | Stirling cycle | Atkinson cycle | Lenoir cycle | d |  Lenoir cycle is one of the idealized thermodynamic air standard cycles which is used in the pulse jet engines. |
Comments | Active | |
| 55 | The effect of regeneration on efficiency and work output of Brayton cycle is that its | Efficiency decreases but work output increases | Efficiency as well as work output increases | Efficiency increases but work output remains same | Efficiency remains same but work output increases | b | Utilization of exhaust gas to preheat the air which is going to combustion chamber.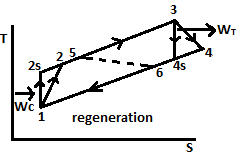 1 – 2S (WC) 3 – 4S (WT) During reg \(η ↑\) While remains same \(W_{T}-W_{C}\) |
Comments | Active | |
| 56 | A gas turbine plant operates between 27°C, minimum temperature and 927°C maximum temperature. Calculate the cycle efficiency | 25% | 50% | 75% | None of the above | d | \( T_{L}=27℃=273+27=300 K\) \(T_{H}=927℃=273+927=1200K\) Remember pressure Ratio \(r_{P}=(\frac{T_{max}}{T_{min}})=rP(ν-1)/ν\) \(efficiency η_{brayton}=1- \frac{1}{rp\frac{γ-1}{γ}}\) \((\frac{1200}{300})=\frac{T_{max}}{T_{min}}\) \(η=1-\frac{1}{4}\) \(η=\frac{3}{4}=0.75=75%\) |
Comments | Active | |
| 57 | For a steady flow system (where kinetic and potential energies are negligible), the first law of thermodynamics can be expressed as | dQ – dW = dU | dW - dQ = dU | - = \(Q\) \(w\) \(∆U\) | - = \( Q\) \(w\) \(∆H\) | d | \( Q-W=H_{2}-H_{1}=∆H\) | Comments | Active | |
| 58 | A machine produces 100 kJ work by consuming 100 kJ heat. This machine will be called | PMM – I | PMM - II | PMM - III | None of the above | b | Here input = output, hence efficiency will be 100% which is PMM II, It violates the 2nd law of thermodynamics.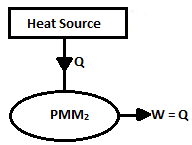 PMM II is a machine which produces work from a single heat source. In this kind of perpetual motion machine there is only one heat reservoir, and it is being spontaneously cooled generating work without heat transfer to a cooler reservoir. The prototype machine of this kind was the ammonia motor (called zero Motor) proposed in 1880s by John Gomgee. |
Comments | Active | |
| 59 | A refrigerator (COP=2.5) removes energy by heat transfer from freezer at 0°C at a rate of 9000 kJ/hr and rejects energy to the surroundings. Determine power input to the refrigerator | 614.3 kJ/hr | 3600 kW | 659.3 kJ/hr | 1 kW | d | \( COP=\frac{Ref. effect}{W_{input}}\)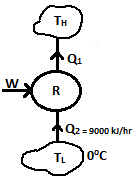 \(2.5=\frac{9000}{W}\) \(W=\frac{9000}{2.5}=3600 kJ/hr\) \(W=\frac{3600}{3600} kJ/sec=1 kW\) |
Comments | Active | |
| 60 | T1 is high and T2 is low temperature of a Carnot heat engine. Which is the most efficient way to increase efficiency? | To increase T1 | To decrease T2 | To increase T1 and T2 both | To decrease T1 and T2 both | b | \( ∴η_{ }=efficiency=1-\frac{T_{sink}}{T_{source}}\) \(=1-\frac{T_{2}}{T_{1}}\) Decrease \(T_{2}, η_{ } will increase\) Increase \(T_{1}, η_{ } will increase\) Let x temperature is decreased from and increased in T, \(T_{2}\) Now \(η_{1}=1- \frac{(T_{2}-x)}{T_{1}}\) \(η_{2}=1- \frac{T_{2}}{T_{1}+x}\) Now \(η_{1}-η_{2}=1- \frac{(T_{2}-x)}{T_{1}}-(1- \frac{T_{2}}{T_{1}+x})\) \(=\frac{-T_{2}-x}{T_{1}}+\frac{T_{2}}{T_{1}+x}\) \(=\frac{T_{2}T_{1}-(T_{1}+x)(T_{2}-x)}{T_{1}(T_{1}+x)}\) \(=\frac{T_{2}T_{1}-T_{1}T_{2}+xT_{1}-xT_{2}+x^{2}}{T_{1}(T_{1}+x)}\) \(=\frac{x(T_{1}-T_{2})+x^{2}}{T_{1}(T_{1}+x)}\) \(∵T_{1}>T_{2} ∴η_{1}-η_{2} will be positive\) \(∴η_{1}-η_{2}>0\) \(=η_{1}>η_{2}\) Now \(η_{2}-η_{1}=\) \(=(1-\frac{T_{2}}{T_{1}+x})-(1- \frac{T_{2}-x}{T_{1}})\) \(=-\frac{T_{1}}{T_{1}+x}+\frac{T_{2}-x}{T_{1}}\) \(=\frac{-T12-(T_{1}+x)(T_{2}-x)}{T_{1}(T_{1}+x)}\) \(=\frac{T12-T_{1}T_{2}+T_{1}x-T_{2}x+x^{2}}{T_{1}(T_{1}+x)}\) \(=(\frac{T12+T_{1}T_{2}+T_{2}x}{T_{1}(T_{1}+x)})+\frac{x(T_{1}+x)}{T_{1}(T_{1}+x)}\) (Greater term) (Smaller term) \(η_{2}-η_{1}=-ve\) \(∴η_{2}-η_{1}<0\) \(η_{2}<η_{1}\) |
Comments | Active | |
| 61 | Gas A at 1 MPa, 100°C and Gas B at 5 MPa, 100°C are mixed such that final temperature after mixing remains 100°(C) The process is adiabatic The entropy of the gases after mixing | Will increase | Will remain same | Will decrease | Cannot be calculated | a | Mixing of gases in an irreversible process and as we known that for irreversible process change in entropy i.e. positive \(∆S>0\) \(∆S=0 for reversible process\) \(∆S <0 impossible process\) |
Comments | Active | |
| 62 | The first law of thermodynamics was given by | Obert | Keenan | Joule | Newton | c | \( Q=W for a cycle\) | Comments | Active | |
| 63 | Pressure compounding can be done in the following type of turbines | Impulse turbines | Reaction turbines | Both impulse and reaction turbines | None of the above | a | Pressure compounding is the method in which pressure in a steam turbine is made to drop in a number of stages rather than in a single nozzle. This method of compounding is used in Rateau and Zoelly tubines i.e. impulse turbine. | Comments | Active | |
| 64 | The following boiler operates in supercritical range of pressure | Benson | Babcock and Wilcox | Loeffler | Cornish | a | Critical point in water vapour cycle is a thermodynamic state where there is no clear distinction between liquid and gaseous state of water, water reaches to this state at a critical pressure above 22.1 MPa and 374℃. Benson boiler acts as super critical boiler. It is once through boiler and converts liquid quickly into steam. | Comments | Active | |
| 65 | Solar photovoltaic cell is made up of semiconductor materials. The efficiency of conversion of solar energy into electrical energy is of the order of | 7% | 21% | 70% | 90% | b | Efficiency is the comparison of energy output to energy input of a given system. For solar photovoltaic (PV) cells. This means the ratio of useful electrical energy they produce to the amount of solar energy incident to the cell under standardized testing conditions. Although some experiment solar cells have achieved efficiencies of close to 50%, most commercial cells are below 30%. Unlike the carnot efficiency which limits the thermal efficiency of heat engines, the efficiency of solar cells is limited by something called the “band gap energyâ€. | Comments | Active | |
| 66 | On increasing the temperature of absorber plate of solar collector the efficiency of collector | Increases | Decreases | May increase or decrease depending upon atmospheric temperature | Does not depend on absorber plate temperature | b | \( η_{collector }âˆ\frac{1}{T_{plate}}\) | Comments | Active | |
| 67 | Absorption of energy in solar collectors can be increased to a maximum value by coating the absorber surface by | Black paint | Lamp black | Rough black coating | Selective coating | d | An optical coating applied to the surface of an element of a solar energy device to reduce thermal radiation losses selective coatings used to increase radiation losses constitute a special group, such coatings absorb solar radiation weakly and have a high emissivity. | Comments | Active | |
| 68 | If B is magnetic field strength, the theoretical power output of MHD generator is proportional to | B | B2 | B3 | \( B\) | b | A magneto hydrodynamic (MHD) generator is a device that generates power directly by interacting with a rapidly moving stream of fluid, usually ionized gases/plasma. MHD devices transform heat or kinetic energy into electrical energy. The typical setup of an MHD generator is that both turbine and electric power generator coalesce into a single unit and has no moving parts, thus, eliminating vibration and noise, limiting wear and tear. MHDs have the highest thermodynamic efficiency as it operates at higher temperature than mechanical turbine. | Comments | Active | |
| 69 | In centrifugal compressors, pressure ratio may be increased | By decreasing slip factor | By increasing slip factor | By making rough blades | By none of the above | a | slip factor \(=\frac{Whirl velocity at the O/L_{\)ideal}}{Whirl velocity at the O/L]_{Actual}}] It reduces energy transfer |
Comments | Active | |
| 70 | Run away speed for Francis turbine ranges | 1.8 to 1.9 times normal speed | 2.5 to 3 times normal speed | 3 to 3.5 times normal speed | 2 to 2.2 times normal speed | d | Runway speed of turbine (speed at no load or at load rejection) Max speed (dangerous) |
Comments | Active | |
| 71 | A centrifugal pump lifts 0.013 water from a depth of 32 m. If the pump motor consumes 6 kW, what is the overall efficiency of pump. Given density of water = 1000 kg/ \(m^{3}/s\) \(m^{3}\) | 88% | 75% | 69% | None of the above | c | \( η_{0})_{pump}=\frac{Water power}{Shaft power}\) \(=\frac{1000×0.013×9.8×32}{6000}\) \(=0.69=69%\) |
Comments | Active | |
| 72 | A Kaplan turbine develops 3000 kW power under a head of 5m and a discharge of 75 m3/s. Determine the overall efficiency | 0.79 | 0.82 | 0.90 | None of the above | b | Overall efficiency \(η_{0}=\frac{Shaft power}{Water power}\) \( =\frac{3000×1000}{1000×75×9.81×5}=0.82\) |
Comments | Active | |
| 73 | A Pelton turbine works under a head of 405 m and runs at 400 rpm. What will be diameter of its runner? ( = 0.45) \(k_{n}\) | 1.93m | 3.80m | 2.10m | None of the above | a | Velocity of wheel \(U=K_{u}2gh\) \(\frac{πDN}{60}=0.442×9.8×h\) \(\frac{πD×400}{60}=0.452×9.8×405\) \(D=1.945 m \) |
Comments | Active | |
| 74 | In C.I. engines, ignition delay can be reduced by | Decreasing compression ratio | Increase in air inlet temperature | Decrease in coolant temperature | Decreasing the engine speed | b | Ignition delay: time interval b/w start of infection and start of combustion. It depends on following factors such as. \(- Ignition delay âˆ\frac{1}{Compression ratio}\) \( âˆinjection timing\) \( âˆ\frac{1}{intake temperature}\) \( âˆ\frac{1}{Output}\) \( âˆ\frac{1}{quality of atomisation}\) \( âˆAuto ignition temperature\) \( âˆ\frac{1}{intake pressure}\) \( âˆ\frac{1}{coolent temperature}\) |
Comments | Active | |
| 75 | Some qualities of C.I. engine fuels are given below. Select the quality which is not desirable | Good ignition quality | High volatility | High viscosity | Low flash point | c | Desirable qualities of fuel of C.I. engine. - Sufficient volatility - Low self – ignition temperature - High cetane rating - Low viscosity - Good ignition quality - High flash and fire point - Low cloud point - Low pour point - Sufficient ignition delay - high density - high calorific value - less content |
Comments | Active | |
| 76 | For atmospheric air, following conditions are given DBT = 35°C, DPT = 23°C and barometer reads 750 mm Hg. Saturation pressure at 23°C and 35°C is 21.06 mm Hg and 42.4 mm Hg respectively. The relative humidity and partial pressure of water vapour will be |
49.7% and 21.06 mm Hg respectively | 35.5% and 42.4 mm Hg respectively | 35.5% and 15.06 mm Hg respectively | Impossible to calculate | a | 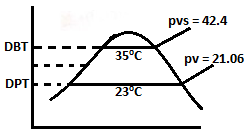 \(RHϕ=\frac{P_{ν}}{P_{νs}}=\frac{21.06}{42.4}=50.01%\) \(P_{ν}=21.06 mm Hg\) |
Comments | Active | |
| 77 | In the concept of effective temperature, the relative humidity of air is considered to be | 0% | 50% | 75% | 100% | b | Effective temperature * It is temperature of saturated environment. * At this point saturated air will be motion less. * It provides human comfort in a normal environment. * Specific valve of DBT, RH and air velocity gives effective temperature. * It is an index Temperature range DBT – 20 – 25℃ Air flow velocity – 5 – 8 m/s Relative velocity – 30% - 70% |
Comments | Active | |
| 78 | When steam is injected into the incoming air, the following changes occur in the condition of air | Temperature increases significantly but specific humidity increases negligibly. | Temperature increases negligibly but specific humidity increases appreciably. | Both temperature and sp. humidity increase appreciably. | Both temperature and sp. humidity increase negligibly. | b | Mainly specific humidity increases. | Comments | Active | |
| 79 | During adiabatic saturation process of air in air washer, the water is sprinkled at a surface temperature equal to _________ of incoming air | DBT | WBT | DPT | None of the above | b | 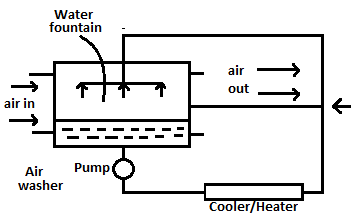 * It is used to condition air * Between air and water heat and mass transfer occur. * Condition of air ∠water temperature  - For cooling and dehumidification \(t_{water}(t_{w}) \(t_{w}=WBT (Process OB)\) Here sensible heat transfer from air to water = Latent heat transfer water to air - For cooling and humidification \(DBT \(t_{w}>DBT (Process OE)\) \(t_{w}>t_{air}\) |
Comments | Active | |
| 80 | A sample of moist air is at a dry bulb temperature of 21°C and dew point temperature of 15°(C) Specific humidity of air is 0.011 kg w.v./kg (d)(a) What will be the enthalpy of moist air? | 59.4 kJ/kg (d)(a) | 323.4 kJ/kg (d)(a) | 52.5 kJ/kg (d)(a) | 49.0 kJ/kg (d)(a) | c | Enthalpy of moist air \(h=C_{P}(DBT)+ω[2500+1.88DBT\)] \(h=1.005(21)+0.011[2500+1.88×21\)] h=49.06 KJ/kg of (d)(a) |
Comments | Active | |
| 81 | Lewis number is given by the following relation: ( fg= heat transfer coefficient, Kw is mass transfer coefficient and Cp is specific heat) | \(\frac{C_{P}}{f_{gK_{W}}}\) | \(\frac{f_{g}}{C_{P-K_{W}}}\) | \(\frac{f_{g}}{k_{w C_{p}}}\) | d | Lewis no \(\frac{Thermal diffusivity }{Mass diffusivity}\) \(=\frac{Schemid^{'}sno}{Prandlt^{'}sno}\) Tells about that fluid flow where mass and heat both are involve(d) \(Le=\frac{thermal conductivity}{sp. head×density×mass transfer coefficient }\) or \(Le=\frac{f_{g}}{ÏC_{P}.k_{w}}\) \(\frac{f_{g}}{C_{P}.K_{w}}\) |
Comments | Active | ||
| 82 | The system used for cooling of supersonic aircraft is | Simple system | Bootstrap system | Reduced ambient system | Regenerative system | d | Regenerative type coding system is used for space shuttle jets, rockets. | Comments | Active | |
| 83 | If F is mass handled by a pump and D is refrigerant vapour distilled in a vapour absorption system, specific weak solution circulation is given by | \(\frac{F}{D}\) | \(\frac{F-D}{D}\) | D/F | \(\frac{F}{F-D}\) | d | \( \frac{F}{F-D}=Circulation ratio\) | Comments | Active | |
| 84 | Aircraft refrigeration system is based upon | Joule cycle | Brayton cycle | Carnot cycle (reversed) | Vapour compression cycle | b |  |
Comments | Active | |
| 85 | If COP of a vapour compression system is 4, the heat rejection ratio of its condenser will be | 0.25 | 5.0 | 1.25 | 0.20 | c | Remember heat reflection ratio \(HRR=1+\frac{1}{COP}=\frac{Q_{rej}}{Q_{add}}\) \(=\frac{Q_{cond}}{R.E}\) \(=1+\frac{1}{4}\) \(=1.25\) Always \(Q_{rej}>Q_{add}\) |
Comments | Active | |
| 86 | External equalizer in thermostatic expansion valve (TEV) is used so that the TEV senses the pressure of evaporator | At the outlet | At the inlet | In the middle | At outlet as well as inlet | b | Thermostatic expansion valve – Controls the flow of refrigerants according to evaporation rate. External equalizer is used to sense the pressure of evaporator and installed after expansion valve and before evaporator (at inlet). |
Comments | Active | |
| 87 | The refrigerant C2H4 is designated as | R 24 | R 15 | R 1150 | R 150 | b | \( C_{m}H_{n}F_{p}Cl_{q}\) \(C_{2}H_{4} can be designated as \) \(R-1 (m-1)(n+1)P\) \(q=2m-(n+P)\) \(m=2, n=4, p=0\) \(R-1150\) \(C_{2}H_{4}=R1150\) |
Comments | Active | |
| 88 | A regenerative liquid – vapour heat exchanger is used in a vapour compression system operating on ammonia refrigerant, the COP | Will increase | Will decrease | Can increase or decrease | Remains unaffected | b | Due to use of heat exchanger, entering condition of refrigerant in compressor will be superheated with NH3, in superheated region COP will always decreases because increment of R.E. is always less than increment of compressor work. | Comments | Active | |
| 89 | In an ammonia vapour compression system, wet compression process is used instead of dry compression. The C.O.P. | Will increase | Will decrease | Can increase or decrease | Remains unaffected | a | In case of NH3, Wet compression will give higher COP because Wet compression Dry compression R.E < R.E WC < WC COPW > COPD |
Comments | Active | |
| 90 | The surrounding air temperature in summer is 45°C in a locality. The refrigeration temperature is 5°C. Assume 10°C temperature difference in the heat exchanger that exchanges heat with surroundings. The COP of the Carnot refrigerator under these conditions, will be | 6.95 | 7.95 | 6.56 | 5.56 | d | \( T_{surrounding}=45℃\) \(∆T with heat exchanger=10℃\) So, source temperature = 45 + 10 \(T_{1}=55℃=328 K\) \(T_{2}=5℃=278 K\)  \(COP_{R}=\frac{T_{L}}{T_{H}-T_{L}}=\frac{T_{2}}{T_{1}-T_{2}}\) \(COP_{R}=\frac{278}{328-278}\) \(COP_{R}=5.56\) |
Comments | Active | |
| 91 | Room sensible heat factor is defined as (RSH: Room sensible heat, RLH: Room Latent heat) | RSH / (RSH+RLH) | RLH / (RSH+RLH) | RSH / RLH | None of the above | a | \(\) \(RSHF=\frac{Sensible heat load}{Total heat load}\) \(=\frac{Q_{S}}{Q_{T}}=\frac{Q_{S}}{Q_{S}+Q_{L}}\) \(=\frac{SHL}{SHL+LHL}\) \(Q_{L}=latent heat load\) Or \(RSHP= \frac{C_{P}(t_{r}-t_{i})}{h_{r}-h_{i}}\) \(t_{r}=room temperature\) \(t_{i}=inlet temperature \) \(h_{r}=room enthalpy\) \(h_{i}=inlet enthalpy\) |
Comments | Active | |
| 92 | In aqua–ammonia and LiBr–Water absorption refrigeration system, the refrigerants are respectively | Water and LiBr | Water and Water | Ammonia and LiBr | Ammonia and Water | d | * Aqua ammonia refrigeration system - Ammonia – Refrigerant - Water – Absorbent * Li Br water absorption system - Water – Refrigerant Li – Br – absorbent * Both are used for above 0℃ refrigeration temperature. * In VARS – instead of compressor, generator, pump and absorbers are used \(W_{VCRS}>W_{VARS}\) |
Comments | Active | |
| 93 | In a simple saturated vapour compression refrigeration cycle, the heat rejected in condenser is 160 kJ/kg and compressor work is 32 kJ/kg, then the COP will be | 4 | 5 | 6 | None of the above | a | By energy balance \(W_{c}+Q_{add}=Q_{rej}\) \(32+Q_{add}=160\) \(Q_{add}=160-32=128 kJ/kg\)  Now \(COP_{rej}=\frac{Q_{add}}{W_{c}}=\frac{128}{32}=4\) |
Comments | Active | |
| 94 | Vapour compression cycle using R-12 gives maximum COP when | Suction state to compressor is in wet region | Suction state to compressor is in superheat region | Suction state to compressor is dry saturated | None of the above | b | 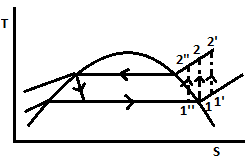 1 – 2 process compression 1 – Dry saturated vapour at inlet 1†– Super heated vapour at inlet 1†– wet vapour at inlet \(COP=\frac{Refrigerating effect}{Compression work}=\frac{R.E}{W_{c}}\) \(1 - 2-RE↓also Wc ↓\) [Compression work of wet vapour decrease] ∵ more than the decrement of RE hence cop decreases. 1’ – 2†– RE ↑ also Wc ↑ [Increment of Wc is greater Than decrement of RE] 1 – 2 – here Cop will be max. |
Comments | Active | |
| 95 | A Carnot refrigeration cycle has a COP of 4. The ratio of higher temperature to lower temperature will be | 2.5 | 2.0 | 1.5 | 1.25 | d | \( COP_{R}=\frac{T_{L}}{T_{H}-T_{L}}=4\) \(\frac{T_{L}}{T_{H}-T_{L}}=\frac{1}{4}\) \(\frac{T_{H}}{T_{L}}-1=\frac{1}{4}\) \(=\frac{T_{H}}{T_{L}}=\frac{5}{4}=1.25\) |
Comments | Active | |
| 96 | A Carnot refrigerator operates between 300.3K and 273K. The fraction of cooling effect required as work input is | 20% | 10% | 50% | Cannot be calculated | b | \( COP_{R}=\frac{T_{L}}{T_{H}-T_{L}}=\frac{273}{300.3-273}\) \(=\frac{2730}{27.3}=10=\frac{RE}{Work}\) |
Comments | Active | |
| 97 | Flat plate solar collectors are used for temperature applications above ambient of about | 20°C | 50°C | 100°C | 1000°C | c | These are used for industrial cooling plant is setup. | Comments | Active | |
| 98 | Most of the terrestrial solar radiations (received on the earth) lie within wavelength range | 0.1 µm to 0.29 µm | 0.29 µm to 2.5µm | 3.8 µm to 7.8 µm | 102 µm to 1010µm | b | Repeated, already discussed | Comments | Active | |
| 99 | Thermal efficiency of closed cycle gas turbine plant is increased by the following | Reheating | Intercooling | Regenerator | None of the above | c | Regeneration: • Regeneration, a process during which heat is transferred to a thermal energy storage device (called a regenerator) during one part of the cycle and is transferred back to the working fluid during another part of the cycle. • In a gas turbine regeneration is done between the exit gas from the turbine and the air coming out of the compressor. • In the regeneration process, there is reduction in heat supplied to the gas but there is no effect on the turbine and compressor work. • Therefore, the regeneration will not increase the work ratio in the turbine but the efficiency of the turbine increases in the regeneration process. |
Comments | Active | |
| 100 | In order to avoid cavitation in centrifugal pumps | The suction pressure should be high | The delivery pressure should be high | The suction pressure should be low | The delivery pressure should be low | a | Cavitation occur when P = pressure \(P_{liq} In pump mainly it occurs at inlet of impeller so suction pressure should be higher. |
Comments | Active | |
| 101 | A low value of time constant for a thermocouple can be achieved by | Decreasing the wire diameter | Using metals of high density and high specific heat | Increasing the heat transfer coefficient | (a) and (c) above | d | Time constant \(=\frac{ÏVc}{hA}=Ï„\) Low value of t can be achieved by - increasing convective heat transfer coefficient. - decreasing diameter of wire i.e. lower surface area (A) - decreasing density of wire . \(Ï\) - decreasing volume V - decreasing specific heat (C) |
Comments | Active | |
| 102 | If the jet ratio in a Pelton turbine wheel is 18, the number of buckets will be about | 24 | 21 | 26 | 18 | a | No of bucket for pelton wheel. \(N_{b}=\frac{Jet ratio}{2}+15\) \( =\frac{18}{2}+15\) \( =24\) |
Comments | Active | |
| 103 | An impulse turbine is used for | Low head of water | High head of water | Medium head of water | High discharge | b | Impulse turbine (Pelton wheel) \(\frac{high head}{Low discharge}\) Reaction turbine – Francis, Kaplan etc. Medium to low head Medium to high discharge |
Comments | Active | |
| 104 | Carbon deposit on the cylinder head of an I.C engine tend to increase | Clearance volume | Compression ratio | Swept volume | None of the above | b | \( r=\frac{V_{c}+C_{s}}{V_{c}} , V_{c}↓, r ↑\) Deposited carbon on cylinder heat of an I.C engine (i) Increases compression ratio (ii) Decrease fuel efficiency (iii) Increases pollution (iv) Contaminate engine oil (v) Decrease ring life (vi) Decrease spark plug life |
Comments | Active | |
| 105 | The injection pressure in diesel engine is of the order of | 30 – 40 bar | 100 – 150 bar | 200 – 300 bar | 400 – 600 bar | c | Pressure range in 200 – 300 bar. | Comments | Active | |
| 106 | Anti-knock property of C.I. engine fuel can be improved by adding | Tetra – ethyl lead | Amyl nitrate | Hexadecane | Trimethyl pentane | b | Tetra ethyl lead can improve anti knocking but very hazardous for environment. Amyl nitrate is a good substitute. | Comments | Active | |
| 107 | If the compression ratio is increased in S.I. engine, the knocking tendency will | Increase | Decrease | Not be affected | Cannot be predicted | a | Comments | Active | ||
| 108 | Loss of head due to friction to maintain 0.05 of discharge of petrol (sp. gravity 0.7) through a steel pipe 0.2 m diameter and 1000 m long, taking coefficient of friction 0.0025 will be \(m^{3}/s\) | 0.644 m | 6.44 m | 64.4 m | 644 m | a | Head loss \(h_{f}=\frac{fLV^{2}}{2gd}\) \(f^{1}=friction factor=4f\) \(L=length of pipe\) \(f=coefficient of friction \) \(v=flow velocity\) \(d=diameter of pipe\) \(h_{f}=\frac{4×0.0025×1000×0.05^{2}}{2×10×0.2×10}\) \(=\frac{25×0.25}{10}=\frac{6.25}{10}\) \(=0.625m=0.63m\) |
Comments | Active | |
| 109 | The height of water column corresponding to a pressure equivalent of 60 cm of mercury column will be | 816 cm | 8160 cm | 81.6 cm | 7996.0 cm | a | \( R_{Hg}=R_{water}\) \(Ï_{Hg}×g×h_{Hg}=Ï_{w}×g×h_{w}\) \(h_{w}=\frac{Ï_{Hg}×h_{Hg}}{Ï_{w}}\) \(=\frac{13.6×10^{3}×60×10^{-2}}{10^{3}}=8.16 m\) \(=816 cm\) |
Comments | Active | |
| 110 | In a laminar boundary over a flat plate, what would be the ratio of wall shear stresses and at two sections which lie at distances units and units from the leading edge of the plate \(Ï„_{1}\) \(Ï„_{2}\) \(X_{1}= 2\) \(X_{2}=10 \) | \( Ï„_{1}/Ï„_{2}= 5.0\) | \(Ï„_{1}/Ï„_{2}= (5)^{0.5}\) | \(Ï„_{1}/Ï„_{2}= (5)^{0.25}\) | \(Ï„_{1}/Ï„_{2}= (5)^{0.05}\) | b | As, we know that \(Ï„âˆ\frac{1}{x}\) \(\frac{Ï„_{1}}{Ï„_{2}}=\frac{x_{2}}{x_{1}}=\frac{10}{2}=5\) \(\frac{Ï„_{1}}{Ï„_{2}}=5^{1/2}=5^{0.5}\) |
Comments | Active | |
| 111 | The nominal thickness of boundary layer represents the distance from the surface to a point where | Flow ceases to be laminar | The shear stress becomes maximum | Velocity is 99% of its asymptotic limit | None of the above | c |  |
Comments | Active | |
| 112 | An oil with specific gravity 0.85 and viscosity 3.8 poise flows in a 5cm diameter horizontal pipe at 2.0 m/s. The Reynolds number will be approximately | 224 | 2240 | 22.4 | 22400 | c | \( R_{e}=\frac{ÏVd}{μ}=\frac{vd}{ν}\) \(=\frac{(0.85×1000)×2×5×10^{-2}}{3.8×10^{-1}}\) \(=22.4\) |
Comments | Active | |
| 113 | Hydraulic radius is equal to | Area divided by the square of wetted perimeter | Area divided by the wetted perimeter | Wetted perimeter divided by area | Square root of area | b | \( Hydraulic radius=\frac{Area}{Wetted perimeter}\) | Comments | Active | |
| 114 | The loss of head due to friction in a pipe of uniform diameter in which a viscous flow is taking place is given in terms of Reynolds number, Re as | 1/Re | 4/Re | 16/Re | 64/Re | c | Coefficient of friction (f) \(f=\frac{16}{Re}\) |
Comments | Active | |
| 115 | At what distance (r) from the centre of a pipe of radius (R) does the average velocity occur in laminar flow | r = 0.33 | r = 0.707 | r = 0.50 | r = 0.59 | b | For laminar flow in a circular pipe, the local velocity may be given as...(i)For laminar flow in a circular pipe, the average velocity may be given as Equating (i) and (ii), we get \(u=U_{max}[1-\frac{r^{2}}{R^{2}}\)] \(V=\frac{U_{max}}{2}...(ii)\) ⇒ ⇒⇒r=0.71R \(\frac{U_{max}}{2}=U_{max}(1-\frac{r^{2}}{R^{2}})\) \(\frac{r^{2}}{R^{2}}=1-\frac{1}{2}\) \(r^{2}=0.5R^{2}\) |
Comments | Active | |
| 116 | In a turbulent flow through a pipe, the shear stress is | Maximum at the centre and decreases linearly towards the wall | Maximum at the centre and decreases logarithmically towards the wall | Maximum mid–way between the centre line and the wall | Maximum at the wall and decreases linearly to zero at the centre | d | Turbulent flow: * Random, disordered, disorganized flow * Bulk mixing * For a pipe Re > 4000 is for turbulent flow. Shear stress varies as  \(τ=τ_{0}\) At r = 0 \(τ=0\) \(at r=R\) \(τ_{max}=τ_{0}\) |
Comments | Active | |
| 117 | When a fluid flows through a pipeline under viscous flow conditions, the ratio of velocity at the axis of the pipe to the mean velocity of flow is | 0.5 | 1.0 | 1.67 | 2.0 | d | 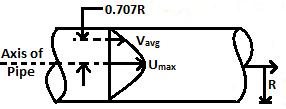 \(\frac{U_{max}}{V_{avg}}=2\) |
Comments | Active | |
| 118 | Navier – Stoke’s equation is concerned with | Turbulence | Viscosity | Buoyancy | Compressibility | d | It describes the flow of incompressible fluid. \(\frac{∂u}{∂t}+u∇u=-\frac{∆P}{Ï}+u∇^{2}u\) \(u=fluid velocity\) \(∆P=Pressure change\) \(Ï=Fluid density\) \(∇=laplocian operator \) |
Comments | Active | |
| 119 | Unit of kinematic viscosity is | /s \(m^{2}\) | N.s/m2 | kg/s.m2 | m/kg.s | a | Kinematic viscosity \(ν=\frac{absolute viscosity}{density}\) \(=\frac{μ}{Ï}=\frac{\frac{N-S}{m^{2}}}{\frac{kg}{m^{3}}}=\frac{\frac{kg-m}{s^{2}}.s.m.}{kg}\) \(=m^{2}/s\) |
Comments | Active | |
| 120 | An oil having kinematic viscosity 0.25 stokes flows through a pipe of 10cm diameter. The flow will be critical at a velocity of about | 0.5 m/s | 1.5 m/s | 1.8 m/s | 4.6 m/s | a | \(\) \(Re=\frac{Vd}{μK}=\frac{2300×0.25×10^{-4}}{10×10^{-2}}\) \(=0.575 m/s\) |
Comments | Active | |
| 121 | Thermal efficiency of a Carnot engine is 30%. If the engine is reversed to operate as heat pump with same operating conditions, what will be the COP of the heat pump? | 0.3 | 1.33 | 2.33 | 3.33 | c | Remember this formula \(cop=\frac{1-η_{ }}{η_{ }}=\frac{1-0.3}{0.3}\) \(=\frac{0.7}{0.3}=2.33\) |
Comments | Active | |
| 122 | Air standard efficiency of an Otto cycle having compression ratio 4 and adiabatic exponent for air r =1.5 will be | 50% | 75% | 25% | 5.0% | a | \( η_{otto}=1-\frac{1}{r^{γ-1}}\) r = compression ratio \(η_{otto}=1- \frac{1}{4^{1.5-1}}=1- \frac{1}{(4)^{1/2}}\) \(=0.5=50% \) |
Comments | Active | |
| 123 | Which dimensionless number has the significant role in forced convection | Mach number | Reynold number | Prandtl number | Pecklet number | b | Comments | Active | ||
| 124 | Fouling factor in the design of heat exchanger is used considering the fact that | It is used when a liquid exchanges heat with gas | it is used in case of Newtonian fluids | It is used as a dimensionless factor | It is a factor of safety in design | d | A fouling factor accounts for the gradual buildup of deposits on the heat exchanger surface, which reduces the heat transfer efficiency, so it is incorporated into the design to ensure the heat exchanger performs adequately even with some level of fouling. | Comments | Active | |
| 125 | In a counter flow heat exchanger, the hot fluid is cooled from 110°C to 80°C by a cold fluid which is heated from 30°C to 60°C LMTD for the heat exchanger will be | 80°C | 50°C | 30°C | 20°C | b | Counter flow heat exchanger LMT(D) \(=\frac{ΔT_{1}-ΔT_{2}}{ln (\frac{ΔT_{1}}{ΔT_{2}})}\) \(ΔT_{1}=T_{ni}-T_{co}=110-60=50℃\) \(∆T_{2}=T_{no}-T_{ci}=80-30=50℃\) \(∴∆T_{1}=∆T_{2}\) \(∴LMTD=∆T_{1}=∆T_{2}=50℃\) * It occurs with the case of counter flow only. |
Comments | Active | |
| 126 | Free convection heat transfer is significantly affected by | Reynolds number | Grashof number | Prandtl number | Stanton number | b | Grashof no. \(Gr=\frac{gβ(T_{S}-T_{∞})Lc3}{ν^{2}}\) For free convection \(N_{u}=f(Gr, Pr)\) |
Comments | Active | |
| 127 | The intensity of solar radiation on earth is of the order of | 1 kW/m2 | 2 kW/m2 | 3 kW/m2 | 4 kW/m2 | a | Radiation which reaches to earth is known as solar irradiance. Total emission from sun = \(3.8×10^{26} W\) Surface area of earth = \(4πRe^{2}\) \(4πRe^{2}=4π(1.5×10^{11})^{2}m^{2} \) \( =28.27×10^{22} m^{2}\) Irradiance = \(\frac{3.9×10^{4}×10^{22}}{28.27×10^{22}}\) \(=1379.55 W/m^{2}\) \(=1.4 KW/m^{2}\) |
Comments | Active | |
| 128 | In turbulent film wise condensation on a vertical surface, the critical value of Reynolds number recommended for use is | 2300 | 1800 | \( 5×105\) | 1000 | b | 1800 for perfect transition from laminar to turbulent. | Comments | Active | |
| 129 | For radiation between two large parallel plates having emissivities the effective emissivity will be \((ϵ_{1}) and (ϵ_{2}) \) | \(∈_{1}+∈_{2}\) | . \(∈_{1}\) \(∈_{2}\) | \(\frac{1}{∈_{1}}+\frac{1}{∈_{2}}\) | \(\frac{1}{\frac{1 }{∈_{1}}+ \frac{1}{∈_{2}}-1}\) | d | Repeated, Already discussed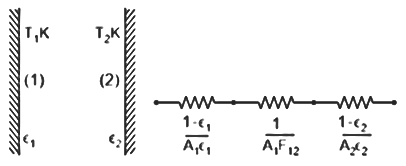 \(q=\frac{σ(T14-T24)}{\frac{1}{ϵ_{1}}+\frac{1}{ϵ_{2}}-1}\) The interchange view factor is \(\frac{1}{R}\) where R is the thermal resistance \(R=\frac{1}{ϵ_{1}}+\frac{1}{ϵ_{2}}-1\) Where and are the emissivities of surfaces 1 and 2. \(ϵ_{1}\) \(ϵ_{2}\) |
Comments | Active | |
| 130 | LMTD in case of counter flow heat exchanger as compared to parallel flow heat exchanger is | Lower | Higher | Same | Unpredictable | b | Log Mean Temperature Difference (LMTD): In a heat exchanger, the temperatures of the heating and cooling fluids do not remain constant but vary from point to point along the length of the heat exchanger. The LMTD of the counter-flow heat exchanger is always greater than the LMTD of the parallel flow heat exchanger. | Comments | Active | |
| 131 | According to Wien’s law, the wavelength corresponding to maximum energy is proportional to | T -1 | T -2 | T -3 | T -4 | a | If sun’s radiation is maximum then wavelength (memorise it) \(λ_{max}=4753 Ã…\) Now Wein’s law says \(λ_{max}âˆ\frac{1}{T} \) \(λ_{max}=\frac{constt}{T}\) |
Comments | Active | |
| 132 | Assuming the Sun to be a black body emitting radiation with maximum intensity at, the surface temperature of the sun will be | 491.4 K | 4914 K | 49140 K | 491.4° C | b | If sun’s radiation is maximum then wavelength (memorise it) \(λ_{max}=4753 Ã…\) Now Wein’s law says \(λ_{max}âˆ\frac{1}{T} \) mK (meter kelvin) \(λ_{max}.T=b=2.892×10^{-3}\) \(T=\frac{2.892×10^{-3}m-K}{4753×10^{-10}m}=6084 K\) [In option only (b) is nearer to ans.] |
Comments | Active | |
| 133 | The value of Stanton number for value of Nusselt number 400, Reynolds number 40 and Prandtl number 20 will be | 800 | 200 | 2 | 0.5 | d | For forced convection heat transfer Stanton number (St) = \(\frac{N_{u}}{Re.Pr}=\frac{400}{40×20}=8.5\) |
Comments | Active | |
| 134 | A body cools from 90°C to 70°C in 5 minutes. The time required by body for further cooling to 50°C will be | 5 minutes | Less than 5 minutes | More than 5 minutes | 10 minutes | a | As, \(Qâˆâˆ†T\) \(∆T_{1}=90°-70°=20°C\) \(∆T_{2}=70°-50°=20°C\) As, the temperature difference is same so, heat transfer will remain same so, it takes some time as 5 min. |
Comments | Active | |
| 135 | A composite wall consists of three different materials having thermal conductivities K, 2K and 4K respectively. The ratio of temperature drop across different materials will be | 1: 1: 1 | 1: 2: 4 | 4: 2: 1 | 2: 4: 1 | c | Fourier’s law of conduction \(Q=-KA\frac{dT}{dx}\) Here \(dTâˆ\frac{1}{K}\) So if \(K_{1}:K_{2}:K_{3}=1:2:4\) Then \(∆T_{1}:∆T_{2}:∆T_{3}=4:2:1\) |
Comments | Active | |
| 136 | The thickness of thermal boundary layer is equal to hydrodynamic boundary layer when Prandtl number is equal to | 0 | 0.1 | 1.0 | 10 | c | \( \frac{δ_{thermal}boundary}{δ_{hydrodynamic boundary}}=Pr^{1/5}\) then \(if P_{r}=1\) \(δ_{t}=δ_{h}\) |
Comments | Active | |
| 137 | If the ratio of emission of a body to that of a black body at a given temperature is constant for all wavelengths, the body is called | Black body | Gray body | White body | Opaque body | b | (Emissivity of body) if for all wavelength is constant then this body is known as grey body. \( \frac{E_{body}}{E_{black}}=E_{body} \) \(E_{body}\) | Comments | Active | |
| 138 | Critical radius of insulation for sphere is equal to | 2k.h | h / 2k | 2k / h | k.h | c | \( r_{cr}_{sphere}=\frac{2K}{h}\) \(r_{cr}_{Cycle}=\frac{K}{h} \) |
Comments | Active | |
| 139 | The thermal efficiency of an ideal Otto cycle | Increases with compression ratio | Increases with specific heat ratio | Increases with compression ratio and specific heat ratio | Increases with compression ratio but decreases with specific heat ratio | a | Comments | Active | ||
| 140 | Change in entropy for a natural process will always be | Zero | Positive | Negative | Undefined | b | Since all natural process are irreversible, hence \(∆S>0 (Always)\) If reversible process. \(∆S=0, \) If impossible process. \(∆S<0,\) |
Comments | Active | |
| 141 | A heat engine receives 1120 kJ of heat and rejects 840 kJ of heat while operating between two temperature limits of 560 K and 280 K. It indicates that the engine operates on the following cycle | Reversible cycle | Irreversible cycle | Impossible cycle | Unpredictable cycle | b | Efficiency of given engine \(η=1-\frac{Q_{rej}}{Q_{add}}\) \( =1-\frac{840}{1120}=1-0.75\) \( =0.25\) Carnot efficiency \(η_{c}=1-\frac{T_{Lower}}{T_{higher}}\) \( =1-\frac{280}{560}=\frac{1}{2}=0.5\) So engine is possible and so engine is not reversible i.e. irreversible. \(∵η<η_{c}\) \(η≠η_{c}\) |
Comments | Active | |
| 142 | For same value of compression ratio and heat input, the order of thermal efficiency of Otto, Diesel and Dual cycles will be as under | > > \(η_{otto}\) \(η_{Diesel}\) \(η_{Dual}\) | ðœ‚Otto > ðœ‚Dual > ðœ‚Diesel | ðœ‚Diesel > ðœ‚Dual >𜂠Otto | 𜂠Dual > ðœ‚Diesel > ðœ‚Otto | b | For the same compression ratio and heat input, the order of thermal efficiency for Otto, Diesel, and Dual cycles is: Otto > Dual > Diesel; meaning the Otto cycle will be the most efficient, followed by the Dual cycle, and then the Diesel cycle with the lowest efficiency. | Comments | Active | |
| 143 | In Carnot cycle, addition and rejection of heat takes place at | Constant pressure | Constant temperature | Constant volume | Constant speed | b | \( Q_{add}-(3-4) T=C\) \(Q_{rej}-(1-2) T=C\) 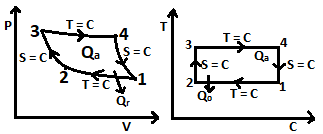 1 – 2 – Isothermal compression 3 – 4 – Isothermal expansion |
Comments | Active | |
| 144 | A heat engine develops 60 kW work having an efficiency of 60%, Amount of heat rejected will be | 400 kW | 10 kW | 40 kW | 20 kW | c | \( η_{HE}=\frac{WD}{Heat supplied} \) \(0.6=\frac{60}{Q_{1}}\) \(Q_{1}=\frac{60}{0.6}=100 kW\) 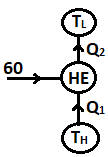 Heat Rejected \(Q_{2}=Q_{1}-W\) \( =100-60\) =40 kW |
Comments | Active | |
| 145 | Area under the curve of a T-S diagram represents | Heat transfer for a reversible process | Heat transfer for an irreversible process | Heat transfer for all processes | None of the above | a | \( TS_{1}S_{2}dS=Q_{1-2}\) Or \((d)Q=TdS\) Or \(Q=T∆S\)  According to entropy definition \(\frac{(d)Q}{T}≤dS\) For reversible process \(dS=\frac{(d)Q}{T} \) |
Comments | Active | |
| 146 | For a process, the value of is \((δQ- δW)\) | Positive | Negative | Zero | Unpredictable | c | For a cycle process 1st law of thermodynamics \(dw=d.Q\) Note: In question “cycle†word is misery. |
Comments | Active | |
| 147 | An engine operates between temperature limits 900 K and T2 and another between T2 and 400 K. For both engines to be equally efficient T2 should be | 600 K | 700 K | 625 K | 650 K | a | Efficiencies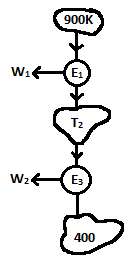 \(η_{E}_{1}=1-\frac{T_{2}}{900}\) And \(η_{E}_{2}=1-\frac{400}{T_{2}}\) Given \(η_{E_{1}}=η_{E}_{2}\) \(1-\frac{T_{2}}{900}=1-\frac{400}{T_{2}}\) \(T_{2}=900×400\) \(T_{2}=30×20=600K\) |
Comments | Active | |
| 148 | For an adiabatic process, the temperature and pressure are related as under | = \(\frac{T_{2}}{T_{1}}\) \((\frac{p_{2}}{p_{1}})^{\frac{r}{r-1}}\) | = \(\frac{T_{2}}{T_{1}}\) \((\frac{p_{2}}{p_{1}})^{\frac{r-1}{r}}\) | = \(\frac{T_{2}}{T_{1}}\) \((\frac{p_{2}}{p_{1}})^{\frac{1}{r-1}}\) | = \(\frac{T_{2}}{T_{1}}\) \((\frac{p_{2}}{p_{1}})^{\frac{r+1}{r}}\) | a | For adiabatic process \(PV^{γ}=c\) Now PV = RT \(∴P (\frac{RT}{P})^{γ}=C\) \(P^{1-γ}.T^{γ}=\frac{C}{R^{γ}}=constent \) \((\frac{T_{1}}{T_{2}})^{γ}=(\frac{P_{2}}{P_{1}})^{1-γ}=(\frac{P_{1}}{P_{2}})^{γ-1}\) \(\frac{T_{1}}{T_{2}}=(\frac{P_{1}}{P_{2}})^{(γ-1/γ)}\) Or \(\frac{T_{2}}{T_{1}}=(\frac{P_{2}}{P_{1}})^{\frac{γ}{(γ-1)}}\) |
Comments | Active | |
| 149 | During throttling process the following holds good | Enthalpy does not change | Entropy does not change | Internal energy does not change | Volume change is negligible | a | The process in which high pressure fluid is converted into lower one is called throttling. Here enthalpy h = constt Workdone W = 0 Ideally this process is isothermal |
Comments | Active | |
| 150 | For non-flow closed system the value of net energy transferred as heat and work equals change in | Enthalpy | Entropy | Internal energy | None of the above | c | For non – flow process (i.e. closed system, 1st law of thermodynamics) \(Q-W=∆U\) |
Comments | Active | |
| 151 | If A = u , B = v and C = \(\frac{δu}{δx}\) \(\frac{δu}{δy}\) \(ʋ\frac{δ^{2}u}{δy^{2}}\) Then momentum equation of the boundary layer given as follows |
+ (B) = (C) Or A + B – C = 0 |
A+B-C=0 | A+B-C2=0 | (A)B=C | b | For laminar flow over plate momentum equation \(u \frac{∂u}{∂x}+v \frac{∂u}{∂y}=ν \frac{∂^{2}u}{∂y^{2}}\) |
Comments | Active | |
| 152 | The necessary data required for the design of the air conditioning apparatus is/are | Grand total heat | Dehumidified air quantity | Apparatus dew point | All of the above | d | Key points for AC design. * Heat load * Air velocity * Quality of air (dryness fraction) * Required temperature * Dew point * Direction of flow * Relative humidity |
Comments | Active | |
| 153 | A refrigerant should have the following property | High boiling point | High latent heat | High specific heat | High specific volume | b | It should have high latent heat so, that it absorb more heat and terns into vapour. | Comments | Active | |
| 154 | Which of the following refrigerant has maximum latent heat? | Sulphur dioxide | Carbon dioxide | Ammonia | Dichloro-difloro-methane | c | Ammonia 1315 KJ/kg Freon – 12 162 KJ/kg Co2 574 KJ/kg So2 381 KJ/kg |
Comments | Active | |
| 155 | Pick up the correct statement | The refrigerant should have high thermal conductivity and low freezing temperature | The refrigerant should have low heat transfer coefficient and high latent heat | The refrigerant should have high specific volume and high latent heat | The refrigerant should have high specific volume and low latent heat | a | Comments | Active | ||
| 156 | Which of the following refrigerant is more costly? | Ammonia | Carbon dioxide | Methyl chloride | Freon-12 | d | Comments | Active | ||
| 157 | Which of the refrigerant is more toxic? | Carbon dioxide | Ammonia | Freon-12 | Freon-22 | b | Comments | Active | ||
| 158 | The refrigeration system works on | Zeroth law of thermodynamics | First law of thermodynamics | Second law of thermodynamics | None of the above | c | Refrigeration system is based on Clausius statement which tells us that heat transfer from low to high temperature is possible only by supplying some work (compressor work) to system.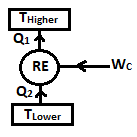 |
Comments | Active | |
| 159 | If the capacity of a refrigerating machine is one ton, than the rate of heat abstraction is equal to | 50 kcal/min | 100 kcal/min | 150 kcal/min | 500 kcal/min | a | 1 to N – 210 kJ/min Heat abstraction = R.E. in kcal/min \(=\frac{210}{4.2}\) R.E. = 50 kcal/min. |
Comments | Active | |
| 160 | The function of a reflector in nuclear power plant is to | Reflect heat | Reflect light | Reflect the escaping neutrons back into the core | None of the above | c | Reflector: Unpuled material region surrounding the core.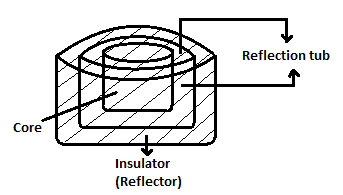 |
Comments | Active | |
| 161 | The gas which is used as a coolant in a nuclear power plant is | Freon | Ammonia | Helium | Chlorine | c | Coolant in nuclear power plant * Water * Heavy water * Air * Co2 * Helium * Liquid sodium etc. |
Comments | Active | |
| 162 | Blade efficiency of steam turbine is equal to | V(Vw1 -Vw2) / 2g | 2V(Vw1-Vw2) / V2 | V(Vw1-Vw2) / V12 | V2(Vw1-Vw2) / 2V1 | b | Blade efficiency = \(\frac{Change in K.E. of steam}{KE applied}\) \(= \frac{Workdone on blades/kg steam}{KE supplied to the blade}\) 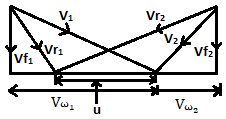 \(m=mass of steam\) \(u=linear velocity of blade\) \(V_{1}=absolute velocity of steam entering\) \(V_{ω_{2}}.V_{ω_{1}}=Whirl velocity at outlet and inlet respectively.\) 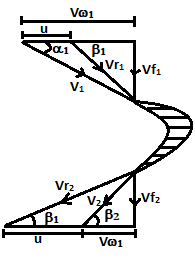 Force on rotor = \(m(V_{ω_{1}}±V_{ω_{2}})\) Work done = \(m(V_{ω_{1}}±V_{ω_{2}}) u\) Blade efficiency \((η_{D})=\frac{m(V_{ω1}-V_{ω2})u}{\frac{1}{2} mv12}\) \(=\frac{2u (V_{ω1}-V_{ω2})}{V12}\) Stage efficiency \((η_{s})=\frac{WD/kg}{Energy supplied/kg}\) |
Comments | Active | |
| 163 | The type of safety valve recommended for high pressure boiler is | Dead weight safety valve | Lever safety valve | Spring loaded safety valve | None of the above | c | Spring loaded pressure relief valves: Generally, the safety valve are refined to the spring loaded pressure – relief valves, the most common type. The load of the spring is designed to press the “Disc†against the inlet pressure. Depending on the fluid type, such as steam, gas or liquid, we are offering a bellows model to clear the back pressure effect. Working Principle * In the normal condition, the downward force due to spring is higher than upward force applied by steam. * The valve is closed due to spring force. * When steam pressure exceeds, the normal limit, upward force due to steam pressure is become higher than downward force due to spring. * Thus the valves are lifted from their seats opening the passages for steam to releases out of boiler. |
Comments | Active | |
| 164 | The capacity of boiler is defined as | The volume of feed water inside the shell | The volume of the steam space inside the shell | The maximum pressure at which steam can be generated | Amount of water converted into steam from 100°C to 110°C in one hour | d | Capacity of boiler: It is the amount of steam converted from water in one hr. from in kg per kg of burnt fuel. \(100℃ to 110℃\) | Comments | Active | |
| 165 | Constant volume gas turbine works on | Joule cycle | Carnot cycle | Otto cycle | Atkinson cycle | d | Atkinson cycle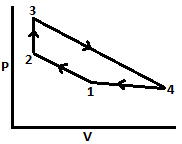  |
Comments | Active | |
| 166 | The thermal efficiency of an open cycle gas turbine increases with the | Increase in inlet temperature of atmospheric air | Decrease in inlet temperature of atmospheric air | Remain same for all temperatures of inlet air | None of the above | b | 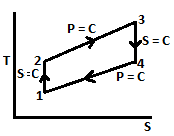 \(η=1-\frac{1}{(r_{p})^{(r-1)/r}}\) \(r_{P}=Pressure ratio\) \(=\frac{P_{2}}{P_{1}}=\frac{P_{3}}{P_{4}}\) and \( \frac{T_{2}}{T_{1}}=(\frac{P_{2}}{P_{1}})^{(r-1)r}\) for isentropic process as \(r_{P}↑, η↑, to increase r_{P}, decrease T_{1} (inlet temperature)\) |
Comments | Active | |
| 167 | The volumetric efficiency of a reciprocating compressor is equal to | 1+K-K( / ) \(p_{2}\) \(p_{1}\) | 1+K-K( / )n \(p_{2}\) \(p_{1}\) | 1+K-K( / )1/n \(p_{2}\) \(p_{1}\) | 1+K-K( / )1/n \(p_{2}\) \(p_{1}\) | c | Volumetric efficiency of a reciprocating compressor. \(η_{vol}=1+K-K(\frac{P_{2}}{P_{1}})^{1/n}\) \(=\frac{actural volume sticked at inlet}{swept volume}\) \(K=clearance ratio\) \(=\frac{V_{clearance}}{V_{swept}}\) \(P_{2}=Delivery pressure \) \(P_{1}=Suction pressure\) As \(K↑, \frac{P_{2}}{P_{1}} ↑, then η_{vol} ↓\) |
Comments | Active | |
| 168 | Which of the following compressors has highest capacity? | Reciprocating | Centrifugal | Axial flow | Fan | b | Reciprocating compressors can be used with 100 tonnes of refrigeration with more than 100 tonnes, centrifugal compressor is used | Comments | Active | |
| 169 | The specific speed of a centrifugal pump is given as | N / \(Q\) \(h^{\frac{1}{4}}\) | N / \(Q\) \(h^{\frac{5}{4}}\) | N / \(Q\) \(h^{\frac{3}{2}}\) | b | Specific speed of a centrifugal pump:- \(N_{s}=\frac{NQ}{H^{3/4}}\) \(Q=discharge=1m^{3}/s\) \(H=1m=head\) \(N_{s}=N\) To produce discharge for 1 m head, required speed is known as specific speed. \(1m^{3}/s\) |
Comments | Active | ||
| 170 | The vanes of a centrifugal pump move due to | Pressure energy of water | Kinetic energy of water | Both pressure and kinetic energy of water | Power supplied by prime mover | d | Power is supplied by prime movers (converts fuel energy to useful work) to centrifugal pump. | Comments | Active | |
| 171 | The type of turbine recommended for a head of 10 meter is | Francis turbine | Kaplan turbine | Pelton turbine | None of the above | b | Head Turbine \(>250 m\) Pleton 45 m to 250 m Francis \(<45m\) Kaplan |
Comments | Active | |
| 172 | The specific speed of a turbine is | Its maximum speed | Its minimum speed | Its speed at maximum output | The speed of a geometrically similar turbine that would develop one metric horse power under a head of one meter | d | Specific speed \((N_{s})=\frac{ NP}{H^{5/4}}\) P = Power = 1 HP H = Head = 1m Then \(N_{s}=N\) To produce 1 HP power for 1 m head, required speed is known as specific speed for a given turbines. |
Comments | Active | |
| 173 | The function of a hydraulic turbine is to convert water energy into | Heat energy | Electrical energy | Atomic Energy | Mechanical energy | d | Turbine converts fluid energy into rotational mechanical energy which is then converted into electrical energy by use of generator. | Comments | Active | |
| 174 | In S.I. engine, the throttle valve of carburettor controls the quantity of | Fuel | Air | Fuel and air mixture | Lubricating oil | a | Throttle valve controls the quantity of fuel supplied. | Comments | Active | |
| 175 | The function of carburettor is to | Refining the fuel | Increase the pressure of fuel vapours | Inject petrol in cylinder | Atomise and vapourise the fuel and to mix it with air in proper ratio | d | To mix air + fuel in spark ignition engine. | Comments | Active | |
| 176 | The function of fuel injector is to | Pump the fuel at high pressure | Mix diesel with air | Atomise the fuel | Ignite the fuel | c | To atomize the fuel and sprayed over hot compressed air in a compressed ignition engine. | Comments | Active | |
| 177 | In a low speed S.I. engine, the inlet valve closes approximately | 40° after BDC | 30° before BDC | 10° after BDC | 10° before BDC | c | 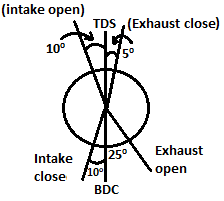 [For law speed engine] |
Comments | Active | |
| 178 | With the help of fins, the heat transfer can be increased by about | 4 times | 6 times | 8 times | 10 times | d | It is definite that due to fins, heat transfer rate increasing readily but without knowing about type of fin its difficult to say. But on average basis we considered it as 10 times. | Comments | Active | |
| 179 | The heat transfer by conduction through a pipe is given by the relation | \(Q=\frac{Ï€Lk(T_{1- T_{2)}}}{logâ¡(\frac{A_{2}}{A_{1)}}}\) | \(Q=\frac{2Ï€Lk(T_{1- T_{2)}}}{logâ¡(\frac{A_{2}}{A_{1)}}}\) | \(Q=\frac{Ï€Lk(T_{1- T_{2)}}}{logâ¡(\frac{A_{1}}{A_{2)}}}\) | \( Q=\frac{2Ï€Lk(T_{1- T_{2)}}}{logâ¡(\frac{A_{1}}{A_{2)}}}\) | b |  \(T_{1}>T_{2}\) As we know that \(Q=\frac{2Ï€ LK (T_{1}-T_{2})}{log (\frac{r_{2}}{r_{1}})}=\frac{2Ï€LK (T_{1}-T_{2})}{log\frac{A_{2}}{A_{1}}}\) |
Comments | Active | |
| 180 | If a body is at thermal equilibrium, then | Emissivity < absorptivity | Emissivity > absorptivity | Emissivity = absorptivity | None of the above | c | At thermal equilibrium, when a body is placed then according Kirchhoff’s law of radiation. Emissivity = Absorptivity \(ϵ_{A}=α_{A}\)  |
Comments | Active |










